Click here to go to 'Figures/Overheads' section.

RETURN TO:

Click here to return to course outline.

Click here to return to W.R. Church's home page.

Click here to return to Earth Science course list.

   REVISION

    ^ means ‘to the power of’; * means ‘multiplied by’; / means 'divided by'

  Major elements: SiO2, TiO2, Al2O3, Fe2O3, FeO, MgO, CaO,Na2O, K2O, P2O5

  Trace elements: Sr; Rb; Ba; Y; Yb; REE; Ti; V; Co; Sc; Zr, Hf; Ta; Nb; Ni; Cr; U; Th

  Volcanic environments: plume, rift, mid-ocean ridge, oceanic arc, back-arc oceanic, fore-arc boninitic, continental arc, komatiite, collision.

    Olivine: (Mg,Fe)2SiO4; forsterite - Mg2SiO4, fayalite - Fe2SiO4;

    %Forsterite in olivine = (Mg/(Mg+Fe))x100 [moles]; compatible trace element - nickel

   Math:   X/Y = 1/(Y/(X+Y)) - 1;     integral of dx/x = ln[x];      x^y = x^(y-1).x;

   Terminology: solidus; liquidus; crystal fractionation;

              Atomic Mass Number, Moles

     The sum of the number of protons and neutrons in an element is known as the 'atomic mass number' of the element, and an 'atomic mass unit' is taken to be 1/12th the mass of an atom of Carbon-12. An 'amu' is therefore effectively  the mass of a proton+electron or a neutron, and weighs 1.66 x 10^-24 grams.
    There are therefore 6.024 x 10^23 [1 / 1.66 x 10^-24] protons/neutrons in one gram of  such material, and this provides the basis of  convenient form of measure whereby one mole of a any substance is taken to be an amount containing 6.024 x 10^23 atoms of the substance.  (Think of a mole as you would think of a basket as a measure of a dozen eggs, a dozen apples, or a dozen oranges, etc.) In the case of Carbon-12 each atom contains 12 atomic mass units (protons/neutrons), and therefore one mole of Carbon-12 is a unit amount that has the mass equivalence of 12 *  6.024 x 10^23  amu.  Given that an amu weighs 1.66 x 10^-24 grams, and given that 1.66 x 10^-24  *  6.024 x 10^23  = 1, this would be equivalent in weight to 12 grams. The weight of one mole of Carbon-12, its gram atomic weight, is therefore simply its atomic mass number expressed in grams.  Similarly, a 'mol(e) of Mg2SiO4'  is a unit amount of Mg2SiO4 containing 6.024 x 10^23 molecules of Mg2SiO4 .  The 'gram molecular weight' of Mg2SiO4 is therefore the mass in grams of 1 mol of Mg2SiO4, that is:

      the number of molecules in one mole * the  number of atomic particles in each molecule * the gram weight of an atomic particle *

                                                    =  6.024 x 10^23  *  [(2 * 24.312) + 28.086 +(4 * 15.999)] * 1.66 x 10^-24
                                                    =                     1    *  [(2 * 24.312) + 28.086 +(4 * 15.999)]

            The Law of Mass Action:

    For the reaction A + B = C + D, where components A and C, and B and D are mutually soluble phases:

   [DG] = [DG₀] + RTln(K) = [ DG0] + RTln ([C].[D])/([A].[B]) where [A], [B], [C], and [D] are the concentrations of components A, B, C, and D, and DG₀ is the difference in the free energy of formation of the products C and D and the reactants A and B as pure phases,

    and when the system is in equilibrium  [DG] = 0, and:

    [DG₀]  =  - RT ln([C].[D]) / ([A].[B]) = -RT lnK where K = [C].[D] / [A].[B]

    If the proportion of A is increased the fractional concentration of C will decrease proportionally, since and A and C are in mutual solution. In this case the product [A].[B] will increase and the product [C].[D] decrease, and consequently the value of K will decrease. However, the reaction of A with B will decrease the concentrations of A and B and commensurately increase the concentration of C and D, thereby tending to increase the value of K.  The reaction of A with B will cease when the value of K returns to the same initial value.

    Imagine components A, B, C, and D have fractional concentrations of .5. then K = [.5] . [.5] / [.5]. [.5] = 1.
    If we increase the proportion of A to .6 the proportion of C must decrease to .4 and K =  [.6] . [.5] / [.4]. [.5] = 1.5.
    Now if the concentration of A decreases to .55 as a result of the reaction of A with B, then the concentration of C will increase to .45, B will decrease to .45, D increase to .55, and the value of K will be  [.55] . [.45] / [.45]. [.55] = 1, the equilibrium value.

        Thermodynamics I
        Thermodynamics II

        Fractionation

        The development of the Earth's continental crust  can be thought of as involving a series of  both singular and continuous  FRACTIONATION  (DIFFERENTIATION)  events.  One of the earliest singular fractionation event in the Earth's history is represented by the formation of the Earth's core, whereas unmixing of the mantle in response to decreasing pressure and/or temperature as hot mantle material convects to levels of lower gravitational potential would represent a continuous first-order melt fractionation event to which the formation of oceanic crust can be directly linked.  Higher order fractionation events involving subduction and arc formation lead to the formation of quartz-feldspar granitoid rocks, whereas fractionation by weathering, glacial action, river transport, wave action,  biological activity, etc, may lead ultimately to the formation of mono-minerallic sedimentary quart arenite deposits,  carbonates,  or salt deposits in isolated stable passive-margin setting.  In a sense therefore the geological history of North America is the history of the higher order fractionation events that have led to the development of the North American continental crust.
        No evidence of first-order fractionation remains in the older geological record. Furthermore, many of the higher order events have been confused as a result of deformation and metamorphism.  Consequently, the first part of this course will be given over to explaining how we can identify the various kinds of  fractionation events, thereby helping us to see through the confusion
         In this lecture I will explain how crystal fractionation influences the composition of igneous rocks, and how  igneous compositional variation  can be used to identify the environment in which the rocks formed.

        Controls on the composition of igneous rocks.

        The composition of igneous rocks derived from a mantle source (mid-ocean ridge, plume, rift, island arc), depends on the following factors:

    1a) The chemical composition of the source material (major and trace elements; H2O and O content).

    1b) The physical conditions (P,T) during melting.

    1c) The mineralogical composition of the source material (e.g. + or - garnet), determined by 1a) and 1b).

    1d) The degree of melting of the source material (low - 1-2%; normal 20%; high - 60%).

    2) The degree of contamination by assimilated crustal material during passage of the melt through the crust.

    3a) The physical conditions (P,T) during near-surface solidification of the melt.

    3b) The degreeof crystal fractionation during solidification.

    3c) The mineralogical composition of the crystallizing material, determined by the chemical compositionof the liquid and by 3a).

           The chemical composition of the melt emerging at the Earth's surface will in part therefore reflect the mineralogical and chemical  nature of the source material. The residual 'source' chemical character  of the rock is known as its environmental ‘fingerprint’. In this lecture I will attempt to establish the simplfied thermodynamic basis for describing the 'compatible/incompatible' behaviour of major and trace elements during crystal fractionation, whereas in a subsequent lecture I will examine the empirical basis of the fingerprinting technique.

    The partitioning of major elements between solid and liquid phases during crystal fractionation, and the concept of element compatibility.

Example: The fractionation of  Fe and Mg during olivine fractionation.

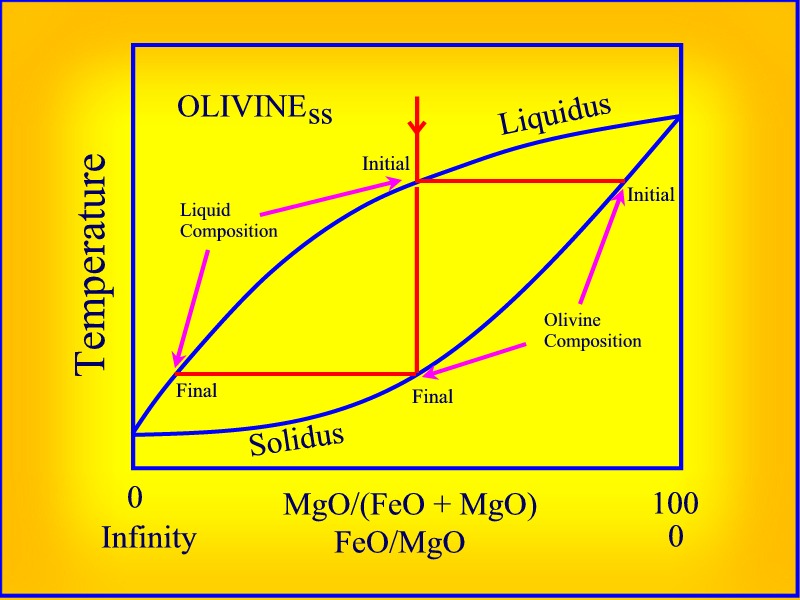
    The composition of olivine is (X,Y)2SiO4, where X and Y represent any fractional molar proportion of Fe and Mg summing to unity. The forsterite and fayalite end members of olivine form a complete solid solution.

    The temperature of a crystallizing melt of  pure forsterite will remain constant until it is entirely solid, as will a melt composed of pure fayalite - although the temperature of solidification will be lower in the case of fayalite. If, on the other hand the olivine melt were composed of a mixture of forsterite and fayalite, it would crystallize over a range of temperatures, and neither the first nor the last crystal to form would be pure forsterite or fayalite.
    The equilibrium crystallization behaviour of olivine (crystals of olivine remaining in equilibrium with the liquid) can be described in terms of the above forsterite-fayalite -temperature phase diagram.  We might assume that the relative amounts of Fe and Mg in the melt and in the olivine in equilibrium in the melt, would be the same. That is, if the melt is 80% forsterite and 20% fayalite, the olivine crystallizing from the melt would be composed of these same proportions of forsterite and fayalite.  However, it is known from empirical and experimental evidence that the first crystals of olivine to form at the liquidus are enriched in forsterite, and that the liquid phase is consequently enriched in fayalite as a result of the crystallization of olivine. Only the last crystal to form would have the composition of the initial melt, and even this would only happen under the condition that the earlier crystallized olivine remain in equilibrium with the progressively iron-enriched melt.

    This relationship can be described in terms of an exchange reaction of the form:

                                                              Mg2SiO4sol+ Fe2SiO4liq = Mg2SiO4liq + Fe2SiO4sol

    The Mg2SiO4sol and Fe2SiO4sol components are in solid solution, and Fe2SiO4liq and Mg2SiO4liq represent the components of the liquid; and when the solid and liquid phases are in equilibrium, then according to the Law of Mass Action:

                                                               K = ((Conc.Fo.liq) * (Conc.Fay.sol)) / ((Conc.Fo.sol.) * (Conc.Fay.liq))

    Since the  molar concentrations of Forsterite in Olivine is:
                                                                           Mg2SiO4 / (Mg2SiO4 + Fe2SiO4) or MgO/(MgO+FeO)
    and the molar concentration of Fayalite:
                                                                             Fe2SiO4/(Mg2SiO4 + Fe2SiO4) or FeO/(MgO+FeO)

then K =( [MgO/(MgO+FeO)]liq*[FeO/(MgO+FeO)]sol)/([MgO/(MgO+FeO)]sol *[FeO/(MgO+FeO)]liq)

    And since                                                 (FeO/(MgO+FeO)) / (MgO/(MgO+FeO)) = FeO / MgO

    and                                                             (MgO/(MgO+FeO)) / (FeO/(MgO+FeO)) = MgO / FeO

    then                                                                K = [FeO/MgO]sol / [FeO/MgO]liq

                                                                                  or K = [Fe/Mg]sol / [Fe/Mg]liq)

    Since we dealing with ratios the equilibrium constant K is known as the distribution coefficient. Otherwise, for single elements, K is known as the partition coefficient.

    Given that the value of K is .33 [1/3] we can easily calculate the FeO/MgO ratio of olivine crystallizing from an olivine melt. Note that since we are dealing with ratios, it would not matter if the melt were to crystallize both olivine and plagioclase; the addition of plagioclase to the system would not change the FeO/MgO ratio of the melt. The fact that the value of K is less than one indicates that Fe 'prefers' to stay in the melt - Fe is relatively incompatible with respect to olivine. As olivine crystallizes therefore, the melt will become enriched in Fe.

    If olivine in equilibrium with a basalt has a composition Fo 84.25 (molar %), and if K (FeO/MgO olivine-melt) = 0.33,  what would be the FeO/MgO [wt% ratio] of the basalt ?
     Answer: Given that [Fe/Mg = 1/Fo - 1]; and that the molecular weight of  FeO = 71.85, and MgO = 40.31, and therefore the weight ratio    FeO/MgO  = 1.78244;  then FeO/MgO Olivine [wt% ratio] = [1/0.8425 - 1]*3*1.78244 = 1

    We can also use this relationship to explain the shape of the liquid solidus phase boundaries of olivine in the above ‘Temperature versus Mg2SiO4 - Fe2SiO4’ phase diagram.

    The curved nature of the phase boundaries would not intuitively suggest that there is a constant relationship between the composition of the olivine and the melt. Nevertheless, if olivine is Fo0 then the FeO/MgO of both olivine and liquid must be infinitely large irrespective of the value of the distribution coefficient, whereas if olivine is Fo 100 then FeO/MgO of both olivine and liquid must be zero. Consequently, the liquidus and solidus phase boundaries must converge towards the extremities of the phase diagram, and between Fo = 0 and Fo = 100 relative FeO/MgO values are constant. The value of the constant determines the shape of the liquidus and solidus curves. This relationship is not intuitively obvious.

    Trace Element compatibility:

    Many trace elements have the ability to substitute for major elements in the structure of mineral phases by processes known as 'camouflage', 'capture' and 'admission' (see Faure page 89 for a discussion of these terms), and the term compatibility refers to the propensity of an element to substitute itself into phases crystallizing from the melt. It is a relative term. For example Ni and Cr are invariably compatible phases, whereas Ba and Rb remain relatively incompatible elements until K-feldspar crystallizes. Other elements whose concentration is linked to the crystallization of specific mineral phases include:

                        Sr; Rb; Ba; Y; Yb; REE; Ti; V; Co; Sc; Zr, Hf; Ta; Nb; Cr; U; Th; Ni

    The trace element that is compatible with olivine is nickel, an element which substitutes for Fe and Mg in olivine.

    In this case we can write the exchange reaction as:

                                                                            MgO ol + NiO liq = MgO liq + NiO ol

                                                                        K =([MgO]liq *[NiO]ol) / ([MgO]ol* [NiO]liq)

                                                                            = ([NiO / MgO]ol) / ([NiO / MgO]liq)

    The exchange relationship can also be written in the form:

                                                                  K = ([ NiO]ol / [NiO]liq) * ([MgO]liq / [MgO]ol)

    and since NiOliq is present only as a trace, ([MgO]liq / [MgO]ol) approximates unity, and

                                                                                        K = [NiO]ol / [NiO]liq

    The experimentally determined value for K (the partition coefficient) is about 12.

    NOTE:  if iron bearing phases such as pyroxene or magnetite are present in the melt then ([MgO]liq / [MgO]ol) would not be unity and K would not be a constant value.

    The compatibility of a trace element can therefore be measured in terms of the value of its partition coefficient, and can vary from a value of 0 (element is totally incompatible and remains in the liquid ) to infinity (element is totally compatible and wholly enters the solid phase). If the value of K is unity, the element show no preference for either solid or liquid.

    How would the concentration of an element vary during crystallization of a melt?

    Having elaborated the concept of partition coefficients, we can now try to understand the way the composition of a melt will vary with degree of crystallization.
    If K [the distribution coefficient) = Cs/Cl [OR Cs=K * Cl] where Cs = the concentration of some element in a solid phase crystallizing from a liquid, and Cl is the concentration of the element in the liquid after the crystallization of a fraction [1-x] of the liquid, and if Co is the concentration of the element in the liquid prior to crystallization, then :

Co = [1-x]*Cs + Cl*x

Co = [1-x]*Cl*K + Cl*x

Co = Cl[[1-x]*K + x]

Cl = Co/[[1-x]*K + x]

OR

Cl = Co/[K-x*[K-1]]

                                                                                    http://publish.uwo.ca/~wrchurch/330/0405mix.htm

    Note 2: The element is not being removed from the system during fractionation but is being merely redistributed between the solid and liquid phases.

If the element is totally incompatible with the crystallizing phase [ie K = 0] what does the equation reduce to ?

    Answer: Cl = Co/x

    If the element is totally compatible [ie K=infinity; remember that infinity - infinity = infinity] what does the equation reduce to ?

    Answer: Cl = 0

    If the concentration of the element in the liquid does not change, what is the value of K?

    Answer: K = 1

        Example:

    If a basalt contains 300 ppm Ni, and olivine in equilibrium with the liquid contains 3600 ppm Ni, and if the relative concentration of Ni in olivine and liquid does not change with crystallization, and if all the olivine stays in equilibrium with the basalt liquid, how much olivine is required to crystallize in order to reduce the Ni concentration of the liquid to 100 ppm.

                                                                 K = 3600/300 = 12, and therefore:

    Ni content of olivine in equilibrium with liquid containing 100 ppm Ni = 1200

100 = 300/[12-x[12-1]]

100 = 300/[12-11x]

300 = 1200-1100x

900 = 1100x

x = 900/1100 = 0.818

        Bulk Partition Coefficients

    If two minerals with K values, Ka and Kb, for the element under consideration, crystallize at the same time in the proportion a/[a+b] and b/[a+b], respectively, where a+b = [1-x], the fraction of solid crystallized, then the above equations can be modified by entering K as the 'Bulk Partition coefficient' where :

          K = Ka*[a/[a+b]] + Kb*[b/[a+b]]

        Rayleigh Fractionation

    If crystallization takes place in infinitesimally small increments, with each increment of solid material being removed from the system as it crystallizes, then the ratio of the concentration of the trace element in the solid phase to the concentration of the element in the residual liquid is K, the partition coefficient, and:

    (dt/dx) / (t/x) = K

    Then:

          dt/t = K * dx/x

      t/t0 = x^K = x^K-1*x

then C/C0 = x^K-1

and C = C0 x^K-1

    Raleigh fractionation can be observed in optically zoned crystals such as plagioclase and zircon. Most minerals, including zoned plagioclase, probably crystallize by some (finite element) incremental process intermediate between Raleigh and bulk fractionation.

FIGURES

Structural Provinces of North America.

RETURN TO:

Click here to return to beginning.

Click here to return to course outline.

Click here to return to W.R. Church's page.

Click here to return to course list.