2) alternatively, by reheating the solidified basaltic crust slighlty above its temperature of solidification and extracting the relatively small amounts of Na, K, and Si enriched melt that forms.
Let us look athe arithmetic of this proposition.
Imagine that the initial liquid contains 0.05% K2O, the least refractory
major element. If we remove 50% of olivine and clinopyroxene from
the melt the concentration will increase to 0.1%. If we remove 50
% of what remains, the concentration will increase to 0.2% and the
remaining liquid will be 25% of the original melt. This relationship
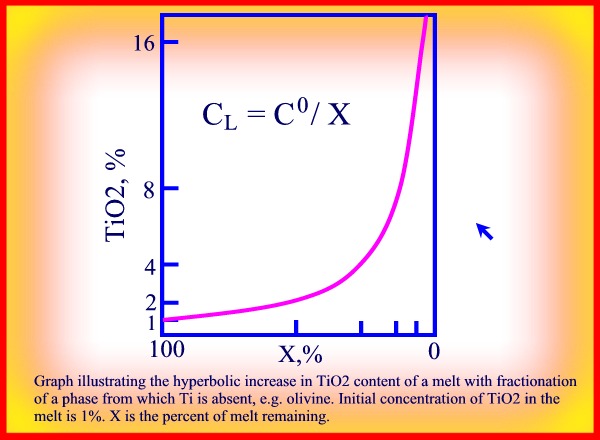
is hyperbolic and is described by the simple equation:
C = C0/x
where C is the present concentration of an element in the residual melt fraction x, and C0 is the original concentration of the element in the melt or source rock. (see Kd)
The graph of this simple equation represents a hyperbolic curve as represented in the following figure showing the behaviour of TiO2 as an incompatible element.
It also follows that if the mantle contains 0.04 wt% K20, and granite contains 3 wt% K2O, the granite would represent only (x = C0/C; x = 0.04/3*100) 1.3 % of the mantle.
If the mantle does not melt entirely but produces a partial melt of basalt
representing 20% of the mantle, the K2O content of the basalt would be
(C = C0/x; C = 0.04/0.2) 0.2 wt%, and to derive
a granite with 3 wt% K2O from a basalt with 0.2 wt% K2O the basaltic
melt would have to be reduced to a residue of (x = C0/C;
x = 0.2/3 = 0.066) c. 7%. That is, 93% of the basalt would
have to be returned to the mantle, and the granite would be still equivalent
to only 1.3% of the mantle (i.e. 6.66% of 20%).
(Note that if the mantle contains as little as 0.01 wt% K2O and the granite
melt or residue contains as much as 4.3 wt% K2O, the granite would
represent as little as (x = C0/C; x = 0.01/4.3*100)
0.23% of the mantle.)
Crystal Fractionation of Basalt, x = C0/C
The following is a sample calculation showing how one might use normative compositions to calculate the proportions of minerals that would crystallize in the during the conversion of basalt to granite by mineral fractionation. The compositions are represented as molar % proportions.
It is normal to present the chemical composition of rocks as 'oxide percent' in the order:
SiO2 TiO2 Al2O3 Fe2O3 FeO MnO MgO CaO K2O P2O5;
or as molar percents of the standard normative minerals:
Ilmenite (Il) Magnetite (Mt) Orthoclase (Or) Albite (Ab) Anorthite (An)
Clinopyroxene (Cpx) Orthopyroxene (Opx) Olivine (Ol)
Quartz (Qtz).
If the normative amount of orthoclase is 2.54 mol% in the primary
basaltic liquid and 12.41 mol% in the residual granite, and if K
has
NOT been fractionated by any of
the crystallizing mineral phases, that is, it is a perfectly incompatible
element, then the granite fraction must represent (x
= C0/C; x = 2.54/12.41) 0.2047 of a unit amount of
primary liquid (i.e. 20.47 mol%), and the crystallized phases must represent
(100 - 20.47) 79.53 mol% of the primary liquid. In other words,
the increase in concentration of orthoclase is purely the effect of the
proportional removal of 79.53% of the liquid as non- K bearing solid phases.
On the basis of this assumption we can therefore determine the proportions
that all the other mineral phases in the residual 20.47% would have if
they also had acted as incompatible elements. If the values calculated
are the same as the concentration in the primary liquid, then the
assumption of incompatibility must be true. If
the calculated values are less than the primary proportion, then the difference
must represent the proportion of the mineral crystallized from the
primary melt.
Measured Measured
Calculated
Calculated
Primary
Residual
Proportion of Proportion of
Basalt, % Granite, %
Residual Granite Crystallized Solid
Il
02.70 -
( 01.32 *
0.2047 = 00.27)
= 02.43 Il
Mt
02.17 -
(03.48 *
0.2047 = 00.71)
= 01.46 Mt
Or
02.54
- (12.41 *
0.2047 = 02.54)
= 00.00
Or
Ab
21.49 -
(21.15 *
0.2047 = 04.33)
= 17.16 Ab
An
32.90 -
(23.50 *
0.2047 = 04.81)
= 28.09 An
Cpx 22.89
- (08.87
* 0.2047 =
01.82) = 21.07
Cpx
Opx 09.86
- (14.82
* 0.2047 =
03.03) = 06.83
Opx
Ol
06.00 -
(00.00 *
0.2047 = 00.00)
= 06.00 Ol
Qtz
00.00 - (13.76
* 0.2047 =
02.82) = -02.82 Qtz
(negative)
Total 100.00
- (100.00 *
0.2047 = 20.47)
= 79.53
Total
We can account for the negative 2.82 mols of quartz by assuming that 2.82 mols of Opx have crystallized as 2.82 mols of quartz and an equivalent amount of olivine. (You will need to think about this!) That is, (6.00 + 2.82) 8.82 mols of Olivine and only (6.83-2.82) 4.01 mols of Opx would have crystallized. These calculations imply that 4 times as much material has been returned to the mantle as is now resident in granitic continental crust.
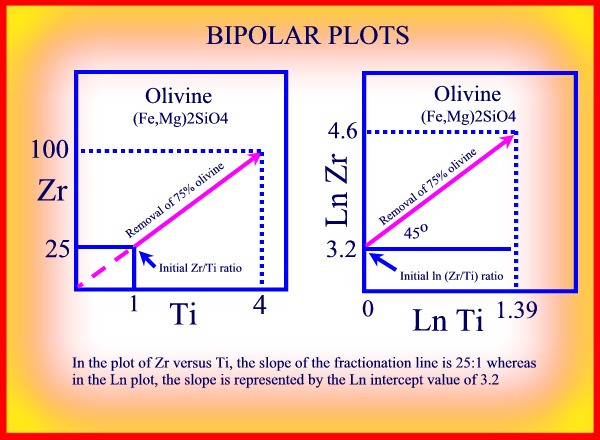
BIPOLAR GRAPHS
When attempting to examine the chemical variation in a suite of rock samples,
it is sometimes more convenient to determine the fractionation vectors
by using bipolar graphs.
Theoretically, in a plot of one incompatible element against another, the
value of the 'initial ratio' of the
two elements will be reflected in the slope of the
line, since in a plot of the concentration
of element 'a', Ca, against the concentration of element
'b', Cb, and where Cao and Cbo
represent the initial concentrations of the two elements:
Ca=Cb.(Cao/Cbo)
The 'initial ratios' can therefore be used to distinguish between two chemically different basalt sequences.
If lon or log values are plotted the slope of the line will be 45 degrees and the initial ratios will be the intercept value of the line, since:
ln Ca = ln Cb+ ln (Cao/Cbo)
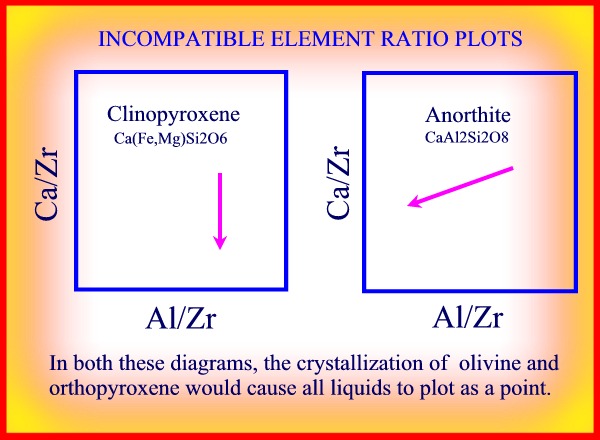
RATIO PLOTS
Ratio plots take away the effect of a simple proportional increase in concentration
due to total mass fractionation. The fractionation effects of specific
minerals can then be recognised by comparing the fractionation trend
with the expected mineral vector variation.
In this case:
Cb/Ca = Cc/Ca * (Cbo/Cco)*(f(Kc,X)/f(Kb,X))
where Ca represents the concentration of a known incompatible
element 'a'; Kc, Kb are partition coefficents
of the elements 'c' and 'b', respectively, and X is the melt proportion.
If a, b, and c are all incompatible elements, then all data values will
plot at a single point, and no trend will be observed on the ratio
plot.
* Draw plots of Ca/Zr v Al/Zr plot when olivine, orthopyroxene, clinopyroxene and plagioclase crystallize successively?