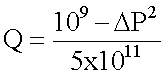
FILTRATION PROBLEM (from Prof C. Briens -Es411a)
A slurry must be filtered with a batch filter which has a filtration area of 14 m2 and a medium resistance of 6x1010 m-1. The slurry has a solids concentration of 10 kg of solids per m3 of filtrate. The filtrate viscosity is 1.1x10-3 N.s.m-2. The cake is incompressible with a specific cake resistance of 1.2x1011 m/kg.
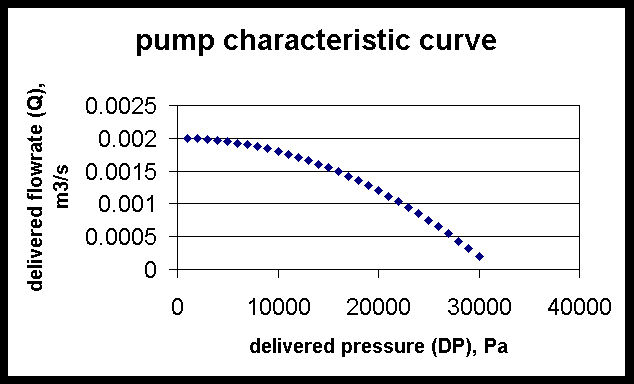
The slurry is delivered with a pump with the following characteristic equation:
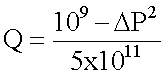
where DP is the delivered pressure in Pa and Q is the flowrate in m3/s.
The pump is directly connected to the filter without any valve nor bypass.
Cleaning the filter takes 6 minutes.
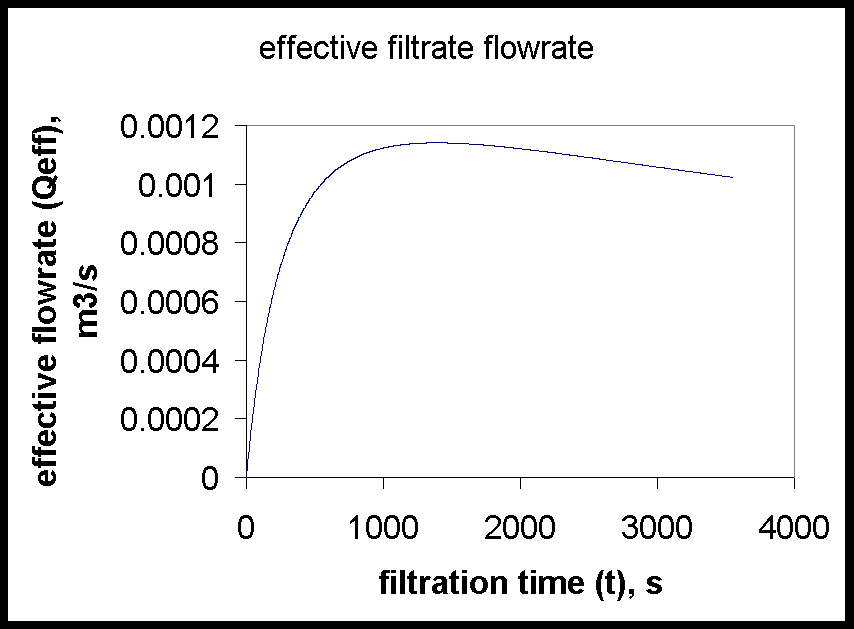
What are the optimum filtration cycle time and the associated effective filtrate flowrate?
ADDITIONAL INFORMATION
Relationship (for an incompressible cake) between the filtrate flowrate Q (in m3/s) and the filter pressure drop DP (in Pa):
Q = A DP / [a m c (V/A) + m Rm]
A: filtration area, m2
c: solids concentration in slurry, kg of solids / m3 of filtrate
Rm: medium resistance, m-1
V: cumulative volume of filtrate (in m3) collected since the start of the filtration cycle
a:
specific cake resistance, m/kgm:
filtrate viscosity, N.s.m-2
To explain the above equation to second year students, you may wish to use an electrical analogy:
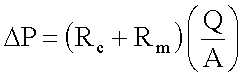
The cake resistance RC and the medium resistance Rm are in series.
Electrical analogy of two resistances in series through which a current i passes under a potential difference DV:
![]()
Q = dV/dt
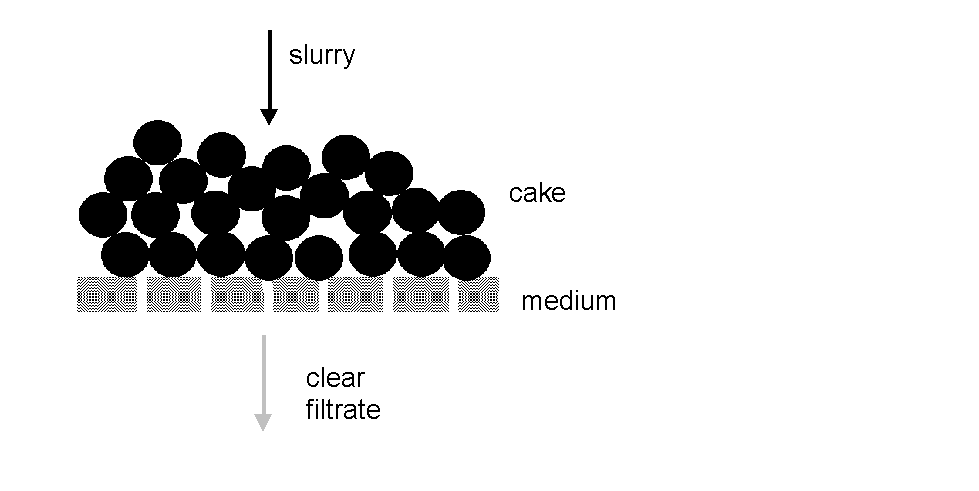
The filtration starts with a clean filter cloth, t = 0, V = 0 and DP = m Rm Q / A.
Since the pressure drop is small at the start of the filtration cycle, the pump encounters little resistance and can nearly deliver its maximum flowrate (see next page)
As the filtration proceeds, the solids accumulate on top of the filter cloth and the resistance of the resulting "cake" of particles increases. The pressure drop DP increases and the flowrate that the pump can deliver against this pressure is reduced.
 From the three equations:
From the three equations:
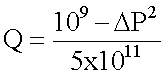
Q = A DP / [a m c (V/A) + m Rm]
Q = dV/dt
One can get the filtration time t required to obtain a volume V of filtrate in a filtration cycle:
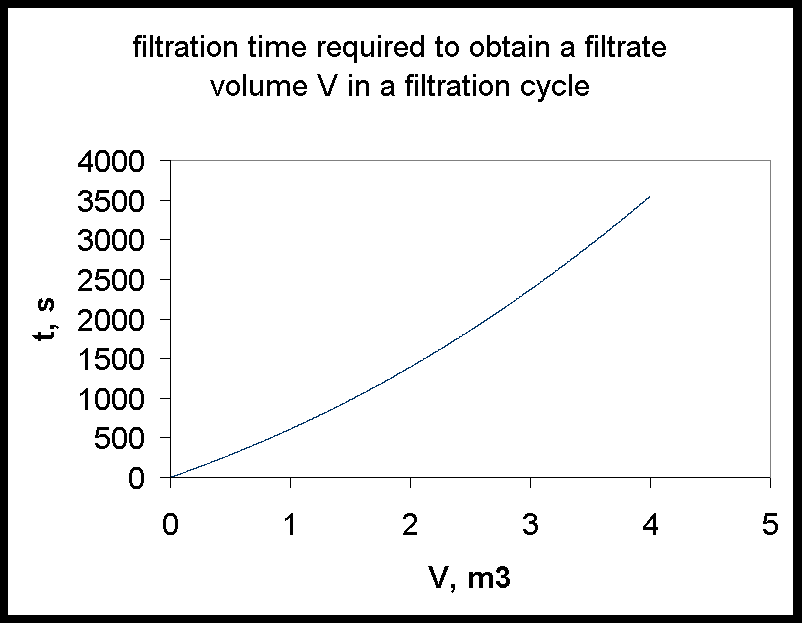
The optimum filtration cycle time t is the time which will give the maximum effective, time-averaged, filtrate flowrate:

where tc is the time required to clean the filter.