|
|
|
|
Designing the full-state feedback
controller
Plotting the closed-loop response
From the main problem, the dynamic equations in state-space form are the
following:
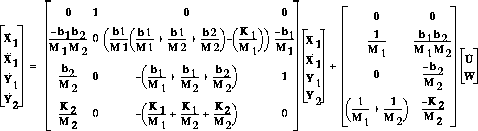
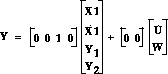
For the original problem setup and the derivation of the above equations, please refer to the Modeling page.
We want to design a feedback controller so that when the road disturbance (W) is simulated by a unit step input, the output (X1-X2) has a settling time less than 5 seconds and an overshoot less than 5%. For example, when the bus runs onto a 10 cm high step, the bus body will oscillate within a range of +/- 5 mm and will stop oscillating within 5 seconds.
The system model can be represented in Matlab by creating a new m-file and entering the following commands (refer to main problem for the details of getting those commands). We need to define the A, B, C, D matrices by entering the following into the m-file:
m1=2500; m2=320; k1 = 80000; k2 = 500000; b1 = 350; b2 = 15020; A=[0 1 0 0 -(b1*b2)/(m1*m2) 0 ((b1/m1)*((b1/m1)+(b1/m2)+(b2/m2)))-(k1/m1) -(b1/m1) b2/m2 0 -((b1/m1)+(b1/m2)+(b2/m2)) 1 k2/m2 0 -((k1/m1)+(k1/m2)+(k2/m2)) 0]; B=[0 0 1/m1 (b1*b2)/(m1*m2) 0 -(b2/m2) (1/m1)+(1/m2) -(k2/m2)]; C=[0 0 1 0]; D=[0 0];
First, let's design a full-state feedback controller for the system. Assuming for now that all the states can be measured (this assumption is probably not true but is sufficient for this problem), the schematic of the system should be:
For this example, we have to use integral action to achieve zero
steady-state error, so we add an extra state which is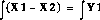 
.
Since in reality the bus will eventually reach an equilibrium that
yields a zero steady-state error. New states become X1, 
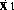Y1, and Y2. Also the state-space matrices, A,B,and C,
after adding extra state change to be the following:
Aa=[0 1 0 0 0
-(b1*b2)/(m1*m2) 0 ((b1/m1)*((b1/m1)+(b1/m2)+(b2/m2)))-(k1/m1) -(b1/m1) 0
b2/m2 0 -((b1/m1)+(b1/m2)+(b2/m2)) 1 0
k2/m2 0 -((k1/m1)+(k1/m2)+(k2/m2)) 0 0
0 0 1 0 0];
Ba=[0 0
1/m1 (b1*b2)/(m1*m2)
0 -(b2/m2)
(1/m1)+(1/m2) -(k2/m2)
0 0];
Ca=[0 0 1 0 0];
Da=[0 0];
Actually, there is a shortcut for matlab to achieve the same result.
Aa = [[A,[0 0 0 0]'];[C, 0]]; Ba = [B;[0 0]]; Ca = [C,0]; Da = D;
Add the above matlab code into the m-file. In this case, we treated the problem like
PID controller design. The integral control is obtained from the new state. The
proportional control is obtained from a gain on Y1 or X1-X2. The
direct derivative control for the output isn't possible, since derivative of
Y1 or X1-X2 isn't a state. Instead we use the derivative of X1
, which is available for feedback. (While X1 maybe hard to measure,
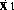could be obtained by integrating the output of an accelerometer
mounted on the bus.) It is similar to adding more damping to velocity of oscillation
of the bus. Add the following matlab code for controller K in the m-file:
K = [0 2.3e6 5e8 0 8e6]We arrive with this value of matrix with trial and error by adjusting gain for derivative of X1,Y1 and integral of Y1, as we previously mentioned.
Looking at the schematic above again, we see that after adding the K matrix into the system, the state-space equations become:
t=0:0.01:2;
step(Aa-Ba(:,1)*K,-0.1*Ba,Ca,Da,2,t)
title('Closed-loop response to a 0.1 m step')
Running the m-file in the command window, you should see the following plot:
Tutorials
