Lab Seven: Correlation and Regression¹

Objectives:

To learn how to find the relationship between paired variables using linear least squares regression, and to quantify the strength of the relationship using Pearson product-moment correlation. To be able to test the significance of the regression and correlation.

Background:

The regression and correlation methods covered in this lab are the most commonly applied parametric techniques. There are other, non-parametric techniques, which in many circumstances may be more appropriate. You should bear this in mind when performing correlation and regression.

If the relationship between two variables is linear then a straight line can be drawn through a scatter plot of one variable plotted against the other, and the equation of that line will look like:

where a is the y-intercept (the value of Y when X = 0); b is the slope of the line or gradient (the change in y for unit change in X, or the rise over the run, a and b are called the regression parameters, and they are all that needs to be known about a straight line to define it. Linear regression provides a means of estimating a and b by minimizing the sum of squared deviations of the dependent variable (y) about the line. Implicit in this method of finding a and b is the assumption that all of the scatter about the line (i.e.

 the error) is due to uncertainty in y only - x is assumed to be known with absolute certainty. Also, the values of the dependent variable (y) are assumed to be normal, the variance of y is assumed to be the same for all values of x (this is called the homoscedasticity assumption), the values of the residuals (deviations of y from the regression line) are assumed to be normal and independent of each other. Some of these assumptions may be relaxed if regression is used only for description and not prediction.

Once the regression equation is known (in other words, once a and b have been found), it is a simple matter to plug-in an x value, and find the corresponding y value. Thus the regression equation provides a model describing the relationship between x and y. This is an empirical model, because it is based on observation (data), not theory. The regression parameters can be computed in the following way:

where,

and n is the number of data points.

A good way of visualizing whether or not there is a relationship between two variables, is to make a scatter plot of one against the other - this should always be done. The strength of the relationship between the variables can be quantified using correlation analysis.

Correlation describes the strength of the relationship or degree of correspondence between paired variables. The basic idea in correlation analysis is to look at the amount of scatter about the regression line. Two variables with low scatter will have high correlation and vice versa. The Pearson product-moment correlation coefficient is the most common correlation index. Pearson's correlation coefficient assumes: data are on a ratio or interval scale, the two variables are linearly related, and if it is used inferentially the data must be from a normal distribution. Pearson's correlation coefficient is closely related to the covariance between the two variables. Covariance describes how the variables change together - how they covary. The covariance is:

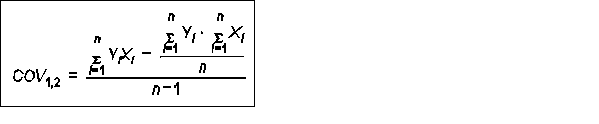
Look up the equation for variance (F²) - Can you see the analogy between covariance and variance? The Pearson correlation coefficient (r) can be computed as shown below.

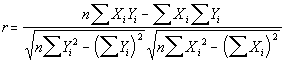
This form of the equation for r appears complex, it is based only on intermediate statistics computed from the raw data, and doesn't require any prior computation of means or deviations. The range of r is from -1 to +1. r values near +1 occur when there is little scatter of data about the regression line, and the variables are related in such a way that an increase in one corresponds to an increase in the other. The regression line has a positive slope: this is called strong positive correlation. r values near -1 also indicate that there is little scatter of data about the regression line, however an increase in one variable corresponds to a decrease in the other - the regression line has negative slope: this is called strong negative correlation. r values near zero indicate a large scatter of data points about the regression line, and weak (or no) relationship between the two variables. Thus, r also serves as an indicator of the reliability of the regression equation, or the "goodness of fit".

One way of assessing the strength of the regression equation is to find the ratio of the variance of the dependent variable from the regression equation (variance of y hat), divided by the total variance of y. This is called the coefficient of determination and is the fraction of variation in y explained by the regression equation. Mathematically, the coefficient of determination is equal to the Pearson correlation coefficient squared (r²).

Significance of Correlation The Pearson correlation coefficient, r, based on a sample of points provides an estimate of the population correlation coefficient, p. In order to test whether or not r is significantly different from 0 (no correlation), a t-test is employed. The null hypothesis is that the population correlation coefficient is zero (H₀: p = 0). This is either a one or two-tailed test. In a two-tailed test, no prior knowledge about the sign of the correlation is assumed, so that the alternate hypothesis states that the population correlation coefficient is not zero (H₁ p ≠ 0). In a one-tailed test, there is basis that the correlation is either positive or negative (H₁: p > 0, or p < 0). The test statistic is:

The degrees of freedom are the number of paired variables minus two (df = n-2). This can be compared with a t-test found from Earickson (Appendix A table 4).

Significance of Regression There are several steps in assessing how "good" a regression equation describes the relationship between two variables. The first is always to plot the data, and the regression line, and look to assess how well the two visually agree. Next you should plot the residuals (y-y hat) to ensure that they are randomly distributed over the range of x. If there is a pattern in the residuals, this indicates that a linear model may be inappropriate. Note here that y hat is the y value predicted from the regression equation, by "plugging in" the corresponding x value while y is the observed y value corresponding to that x value. It is possible to test for any systematic pattern in the residuals using a runs test for randomness . It is possible to determine whether the independent variable (x) accounts for a significant portion of the total variation in the dependent variable (y) using an F test. The observed statistic is:

which you will notice is the square of the t_obs, used for testing the significance of the correlation. The null hypothesis states that the population coefficient of determination is equal to zero (H₀: p² = 0), The alternate hypothesis states that the population coefficient of determination is not equal to zero (H₁ p² ≠ O). There are df₁ = 1 (for between samples variance estimate) and df₂ = n - 2 (for within samples variance estimate) degrees of freedom.

It is also possible to test how significantly different the regression intercept, a, and slope, b, are from some arbitrary value. This involves finding the standard error of a and b and using a t-test. Testing the significance of the intercept, a, is usually not as interesting as testing the significance of the slope, b, since this tells us whether or not the trend implied by the regression equation is meaningful. The formula for the standard error of the slope is:

The null hypothesis states that the population slope ($) is equal to some arbitrary value, usually zero which implies there is no trend in the data (H₀:$= 0). The alternate hypothesis states either that the population slope is not equal to the arbitrary value (0) in which case a two-tailed test is employed; or that the population slope is greater than or less than the arbitrary value in which case a one-tailed test would be employed (H₁ $ ≠ 0 or $ > 0; or $ < 0). The observed statistic for this test is:

where b is the sample slope, and $ is the arbitrarily chosen slope (usually 0). There are n-2 degrees of freedom (df = n-2).

Questions:

You will be using SPSS for Windows, as well as tables and hand calculation in this exercise.

Hand in a printout of your results, as well as written response to the questions where required. You should follow the formal hypothesis testing methodology whenever appropriate (and include this in your write-up.)

1.The data below were obtained from a study of ablation (melting) on a glacier in Swedish Lapland:

Answer the following questions "by hand". Check your answer with SPSS.

(a) Are mean monthly temperature and ablation correlated? What is the correlation coefficient, and is it significant?

(b) Find the regression equation that will allow ablation volume times 10⁵ to be predicted from mean monthly temperature. What is the percentage of ablation explained by mean monthly temperature? Is it significant?

(c) Graph the observed and predicted data and draw the regression line through the predicted points. Graph the residuals.

(d) Comment on the graphs. How good is the overall fit? How could a more precise fit be obtained from this same data set?

3. There continues to be considerable debate in the scientific literature about whether global warming due to increases in greenhouse gases, has yet been detected by the global temperature sensing network.

(a) Using global temperature anomaly data which has been corrected for El Nino / Southern Oscillation influences (see data table 1), find the regression equation describing the temporal trend in global temperature. What is the percentage of temperature change explained by the temporal trend? Is this significant?

(b) Plot the data and the regression line. Plot the residuals. Comment on your plots. Are the residuals randomly distributed?  What does this imply?

(c) Is the slope of the regression line significantly greater than zero (i.e. is there a trend)? Comment on your findings.