Lab Five: The Chi-Square Goodness of Fit Test

The chi-square test can be employed to test whether a set of observed frequencies are consistent with those from a given distribution. The most common tests are for comparisons with the poisson and the normal distributions.

Computational Formulae:

P² = E [ (Observed-Expected)² / Expected ],

for each of k cells in the matrix

Expected = (Row Total ! Column Total) / Grand Total

More formally this is

where k is the number of class intervals, f_o is the observed frequency and f_E is the expected frequency count.

1. To be calculated manually:

This is a nonparametric test, meaning if a good distribution-based test can be applied to your data, such an analysis would be more rigorous (or, as statisticians say, robust). Nevertheless, the chi-square test is very useful, especially when data are nominal. It will probably be most effective to explain the process using an example.

You have noticed that pine trees grow well in some parts of the woods, but not others. You speculate that the distribution of pines is related to drainage, that is, that pines prefer a very well-drained soil, while they do poorly in wet areas. You sample soil from evenly spaced plots throughout the forest, two days after a heavy rain. You discover that there are three categories of soil: dry (sample falls apart in your hand), loamy (holds shape if you squeeze it, falls apart if you drop it), and wet (muddy - you can squeeze lots of water out, soil is muddy).

Let's say you had 100 plots, and you found that 50 were dry, 30 loamy, and 20 were wet. Let's also say that 50 plots had pine trees on them. Now, if soil drainage has no bearing on the distribution of pines, then the distribution of soil types in plots with pines would be expected to be the same as throughout the entire forest, namely, 50% dry, 30% loamy, and 20% wet. Among the 50 plots with pines, then, the expected frequency of soil types would be 25 dry, 15 loamy, and 10 wet. Suppose you observed that 31 were dry, 17 loamy, and only 2 were wet. It looks like there was a tendency for pines to prefer dry soils. Here is how to attach a probability to that apparent tendency.

For each category take the observed frequency (O) and subtract the expected frequency (E). Square the difference and divide by E. Add up the results for the three categories. The total is the Chi-Square statistic.

31 observed dry minus 25 expected dry = 6
6 squared = 36
36 divided by expected frequency E = 36/25 = 1.44

The other two categories gave values of 0.27 and 6.4. The total adds up to 8.11, which is the chi-square value.

The number of degrees of freedom is always one less than the number of O vs. E categories. Since there were three categories, you have two degrees of freedom.

A table of percentage points of the Chi-Square distribution lists numbers called critical values. Compare your value with the tabled values for your number of degrees of freedom. If your value exceeds the tabled value for the probability of 95% (p < 0.05) then the null hypothesis is rejected.

In the example, your value of 8.11 exceeds the table value of 5.991 for 2 degrees of freedom, 95% probability, therefore you can safely reject the null hypothesis - soil drainage did influence the distribution of pines. In fact, your value also exceeded the tabled value for 97.5% (p < 0.025), but not 99% (p < 0.01). Therefore you can say you reject the null hypothesis with a confidence level of p < 0.025. The p value is always the probability that the distribution you saw was due to chance alone, and it is the p-value that is usually reported.

Summary

To conduct a chi-square goodness-of-fit test:

1) Divide your measurements into categories, which can be qualitative characteristics or ranges of numbers.

2) Determine the percent of measurements that should fall into each category, if the null hypothesis is to be supported.

3) Determine the expected number of measurements in each category among your test samples, based on those percentages.

4) List the observed number of measurements for each category.

5)Obtain [(O-E) squared]/E for each category.

6)Add up each separate result to get the chi-square value.

7) Degrees of freedom = number categories minus one.

8) Find the tabled value for 95% (p < 0.05) corresponding to your degrees of freedom.

9)Determine if the chi-squared statistic exceeds the tabled value.

10) If the null hypothesis is rejected, see if it can also be rejected at a lower probability value.

Created by David R. Caprette (caprette@rice.edu), Rice University 8 May 1997

Using P² to compare to a poisson distribution

Example

Number of collisions between passenger trains on British rail, 1970 to 1983

Problem 1: (20 marks)

Lightening strikes per day were recorded in Alberta for 6 summers (July and August).

Calculate using a weighted mean

Calculate the probability P(X) for the number of strikes per day using the Poisson formula:

Now determine if the pattern of lightning strikes is consistent with a Poisson distribution.

Example of testing for ‘normality’

How is the P² goodness-of-fit test calculated to test if observed data are normally distributed?

For instance, one may observe the number of people on some 8-point scale, thus having 8 category intervals and 8 corresponding observed frequencies, as in the table below:

this table calculates the standard deviation for the frequency data. If you are converting from ratio level data you would calculate the standard deviation normally. We need the standard deviation to convert the scale values to standard scores.

mean for grouped data is 

=441/100=4.41

Variance for grouped data is

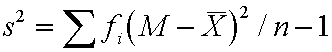
where M is the midpoint of the category and x is the grouped mean

To get percentage of distribution below, we look in a table of values of the normal distribution -- it is the percent of cases which, in the normal table, would fall in a particular category interval or lower (ex., 67% of cases would be expected to fall to the left of z = .44, according to a normal distribution table).

Column 6 shows the percentage of cases falling within a particular scale category. Because in this example the standard deviation, s, is very large (8.11) compared to the range of the data (1 - 8), many cases would be expected to fall in the tails (the 1 and 8 categories) if normally distributed - an unusual situation.

Multiplying the expected percent within times the number of cases (100) gives the expected normal distribution.

Plugging the observed values and the expected values into the chi-square formula allows us to crank out the chi-square value, which is the sum of last column.

Degrees of freedom equal the number of categories (8) minus the restrictions on the data (3: mean, standard deviation, and sample size specified in advance).

For P² equal 58.35 and degrees of freedom equal to 5, a table of P² values shows 58.35 is much larger than the critical value of chi-square for even p=.001. That is, there is less than 1 chance in a thousand that these data do not differ from a normal distribution. We cannot assume these data are normally distributed.

Problem 2 (30 marks)

Test to see if the marks for Geog 301 last term are normally distributed. You will need to convert to standard scores and then group into frequency classes. Use the following frequency intervals: (-∞ to -.6), (>-.6 to .6), and (>.6 to ∞) for the z scores.

66, 67, 71, 80, 71, 62, 82, 57, 87, 70, 60, 74, 85, 91, 64

Now assume you have 5 cases equal to each of the above values.  What happens to the mean, the variance and the P² value?

Problem 3 (50 marks)

Collect a distribution of data that interests you.  Test to see whether it is normally or Poisson distributed. Include your hypotheses and significance level.  You may do it on a computer if you document your steps well.