Lab Four: The 't' and the 'z' Tests

INTRODUCTION

Both the 't' and 'z' parametric tests serve to answer the same research question: does the sample (or samples) come from the same underlying population. Or in other words is the sample mean (X) significantly different from the population mean :. The 'z' test, is used when the standard deviation of the population (F) is known. When information about the population is unknown or when two sample means are being compared, then the 't' test is employed. Both tests assume that the variable measured comes from a normally distributed population and that the samples were selected randomly. It should also be realized that when the number of observations exceed 40, the 't' and 'z' tests are roughly equivalent.

Computational Formulae:

'z' test formulae

(if samples are drawn from an infinite population),

or

(if samples are drawn from a finite population)

(N = number of observations in the sample; N_p = number of observations in the population) .

't' test formulae

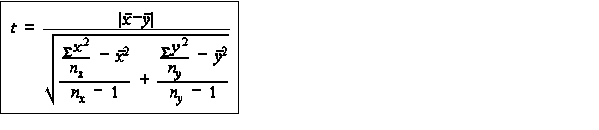
where x  and y  are the means of the two samples and n_x and n_y are the sizes of the two samples. This formula is equivalent to the formula given on page 168 in the textbook. The formula given here is the easiest to use if you are doing the t-test manually. It is not the best to use if your were writing a computer program to do it. If you chose to use the textbook formula you should refer to page 171 for an example.

the degrees of freedom for the t test are given by

you need only use this formula if you are comparing samples from two different populations with extremely large variances.

Therefore don’t use it in this exercise, use df = n₁ + n₂ -2.

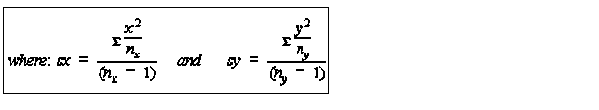
where, x , y are the means of the two samples and n_X and n_y are the sizes of the two samples.

Example of t test for unmatched samples:

Assume a test of map reading skills is given to 35 randomly selected male students and 35 randomly selected female students. A score of 1 indicates low skill and 5 high skill.

Determine if the two groups have statistically different means.

Step 1: Find the mean for each sample

Step 2: Find the variance for each sample

Step 3: Find the standard error of the difference between means

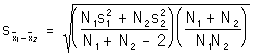
Note this yet another version of the formula for the standard error of the difference between means. All the formulas give an answer of .24. Try it! They are simply different algebraic manipulations for the same formula. This is common when looking at statistics textbooks. You won’t always see the same formulas. Use the one you like the best.

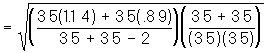
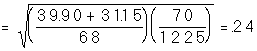
Step 4: Compute the t value from the difference between the means and the standard error of the difference

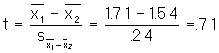
Step 5: Determine the critical value of t

df=N₁ + N₂ - 2 = 35 + 35 - 2 = 68

t=2.00

Step 6: Compare the calculated and table t values. t calculated = .71 which is less than the critcal value of 2.00 so we accept the null hypothesis.

Above example derived from Elementary Statistics in Social Sciences by J. Levin and J. A. Fox, 1991, Harpers Collins Publishers, NY, pp. 210-213.

Example 2: Use of t-test for paired samples

Below is a comparison of murder rates for 5 cities in the US for 1960 and 1970

Determine if there is any difference between 1960 and 1970.

Step 1: H_o: There is no difference in the mean murder rate for 1960 and 1970.

H₁: There is a difference in the mean murder rate for 1960 and 1970.

Step 2: Find d and d²

Step 3: calculate the variance of the mean differences between pairs

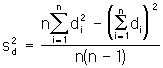
Step 4: calculate t

Step 5: set "=.05 and find t table value for df=3, t = 3.182

we accept H₀

INSTRUCTIONS

Parts 1 and 2 are to be calculated manually with the use of the above formulae, part 3 is to be evaluated using SPSS for Windows.

Part I (20 marks)

From a Canada-wide study that looked at land conversion from rural to urban uses (for all urban areas with a population of more than 25 000 as of 1971), the following sample of Ontario cities was selected.

The question to be answered: are Ontario cities more susceptible to land conversion (meaning conversion to urban from rural or rural to urban) than other- Canadian destinations? Assume that the variable 'Total Area Converted' is normally distributed and that the 72 cities in Canada with a population of at least 25,000 have a mean of 1196 ha of converted land and a standard deviation of 200 ha. In answering, be sure to state:

a) The null and research hypotheses,

b) Whether the test is one-tailed or two-tailed,

c) Which test (the 't' or 'z') should be used and what the calculated value is,

d) At a 95% confidence interval, the critical value as found in the relevant table (see text book), and

e) If the null hypothesis can be rejected.

f) What, then, can be concluded about land conversion in Ontario in comparison to the rest of Canada?

Part 2a (20 marks)

Listed below are the values (in millions of dollars) of Canadian foreign direct investment transactions made in the states of Florida and New York for the years 1989 to 1991. The majority of these transactions are in the form of mergers, acquisitions or new plant openings by Canadian investors.

The question to be answered: is the average value of Canadian foreign direct investment in New York significantly different from that in Florida. Again, in answering, please state the following:

a) The null and research hypotheses,

b) Whether the test is one- or two-tailed,

c) Which test should be used to answer the question and the calculated value attained,

d) At a 95% confidence interval, what the critical value is, and

e) If the null hypothesis can be rejected.

f) What can be said about Canadian foreign direct investment in New York and Florida; is there a significant difference?

Part 2b (20 marks)

Listed in Table 3 are winter wheat yields for some towns in England.

The question to be answered is: did the yields change across time?

a) The null and research hypotheses,

b) Whether the test is one- or two-tailed,

c) Which test should be used to answer the question and the calculated value attained,

d) At a 95% confidence interval, what the critical value is, and

e) If the null hypothesis can be rejected.

f) What can be said about winter wheat yields; is there a significant difference?

Part 3: (20 marks)

Using the same data from Part 2, use SPSS for Windows to confirm your results. Make sure to hand in all output.

a) is the calculated value on the output the same as the one calibrated by hand? If not, account for the difference

b) How does one determine significance solely from the output? (ie. without the aid of any tables or calculations.) With 95% certainty, can the null hypothesis be rejected ?

Part 4: (20 marks)

Using data that you have collected, conduct either a t or z test on two samples.   As usual discuss the imperfections of the data and what they mean and their significance.  Be sure to outline your hypotheses and significance levels before you conduct the test.

Extra Credit: (20 marks)

Using data that you collect yourself, perform a 2-sample Difference of Proportions Test. Provide details of the source of the data and any limitations it might have.

State:

a) The null and research hypotheses,

b) Which test should be used to answer the question and the calculated value attained,

c) At a 95% confidence interval, what the critical value is, and

d) If the null hypothesis can be rejected.