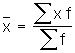Lab Number Six: Non-Parametric Tests :
The Mann-Whitney U-Test, Kruskal Wallis Test, Kolmogorov-Smirnov goodness of
fit test, Kolmogorov-Smirnov 2 sample test
The Mann-Whitney U-test
The Mann-Whitney U-test is a popular non-parametric test that allows for the
statistical comparison of differences between two independent sets of data that
are, at the very least, strongly ordinal. Rather than assuming that both
samples are drawn from populations with normal distributions, it simply tests
the null hypothesis that these two groups are drawn from populations with
identical distributions. In other words, no assumptions are made about the
nature of the distributions.
Computational Formulae:
U1 = n1.n2 + n1(n1 +
1)/2 -GR1
U2 = n1.n2 + n2(n2 +
1)/2 -GR2
where U is the test statistic,
where n1 and n2 are sample sizes,
where R1 and R2 are calculated ranks.
If ranks are tied use the average of the ranks.
Example
A map reading test, which yields only ordinal level data is
given to 8 randomly selected men and eight randomly selected women. Do men
differ from women in terms of map reading? Test with a= 0.05.
|
Men
|
Rank (R1)
|
Women
|
Rank (R2)
|
|
72
|
4
|
81
|
8
|
|
86
|
11
|
80
|
7
|
|
61
|
2
|
45
|
1
|
|
92
|
13
|
96
|
16
|
|
82
|
9
|
93
|
14
|
|
68
|
3
|
85
|
10
|
|
74
|
5
|
90
|
12
|
|
94
|
15
|
75
|
6
|
|
N=8
|
R1= 62
|
N=8
|
R2= 74
|
Find the null and the alternate hypothesis
H0: there is no difference in
male and female map reading
H1: there is a difference in male
and female map reading
Calculate UA and UB
UA= N1 N2+ N1(N1+1)/2 - R1
UA= 8x8+ 8(8+1)/2 - 62
UA= 64+ 36 - 62
UA=38
UB = N1 N2 - UA
UB = 64-38= 26
UB
is the lower value and is therefore compared to the critical value from the
tables which for N1=8
and N2=8
is 13. As the calculated value is greater than this H0 can not be
rejected.
adapted from:
http://www.unn.ac.uk/academic/ss/psychology/resource/py071/ass2/stats/ExampleU/ExampleofMannWhitneyUtest.htm
INSTRUCTIONS (10 marks)
1. To be calculated manually:
The 1986 asset levels of the top nine banks from the United Kingdom, and the
top eight banks from France, are listed below.
Please note that the values of the figures presented are rounded to the
nearest billion and are expressed in US dollars.
British Banks (Top 9)
70 24 123 13 47 14 117 78 39
French Banks (Top 8)
41 116 40 26 156 133 42 143
You are asked to compare these two groups, by employing the Mann-Whitney
U-test. Please answer the following (remember to show all work):
a. State the null (Ho) and the research (H1)
hypotheses.
b. Using both the formal and informal methods, calculate BY HAND the
value of U. (Hint: compare the Test Statistic to the computational
value of U).
c. At the 95% confidence level, what is the critical value of U?
d. Are we dealing with a one- or two-tailed test? Why? Do we accept or
reject the null hypothesis?
2. To be calculated using SPSS for Windows: (10 marks)
Similarly, these are the assets of the top 20 Japanese and German banks, in
$US billions. Again, compare these two groups and answer the following
questions:
German Banks
19 73 133 20 58 76 18 49
32 102 77 15 13 12 10 63
56 17 16 14
Japanese Banks
162 240 191 131 212 205 116 138
78 111 204 81 161 114 73 125
101 124 115 100
a. State the null and the research hypotheses.
b. Using the informal method, calculate the value of U. How does your
answer compare to the SPSS for Windows output? Explain any differences.
c. What is the critical value of U? Assume "
= 0.05.
d. Are we dealing with a one- or two-tailed test? Why? Do we accept or
reject the null hypothesis?
Non-Parametric Tests Part II The Kruskal-Wallis H-Test for K-Samples
Kruskal Wallis Test
Unlike the Mann-Whitney U-Test, the Kruskal-Wallis H-test is designed to
provide a non-parametric alternative to one-way analysis of variance for more
than two sample sets. The assumptions underlying the Kruskal-Wallis H test are
similar to those of the Mann-Whitney U-test. Thus, it is normally applied to
rank-order (ordinal) data, and it does not assume that the samples being tested
are derived from normal distributions. It is important to remember that when
samples of greater than 5 individuals are examined, the Kruskal-Wallis H-test
uses the same critical values as the chi-square distribution. In determining the
degrees of freedom for a given test, simply employ the k-1 correction;
i.e. the number of samples minus 1.
Computational Formulae:
H = 12/N(N+1) . E(Ri²/ni)
- 3(N+1)
1 - E(t3-t)/(n3-n)
Tie Correction (for the purposes of this lab use the average of the tied ranks
if required)
Example
Four different methods of growing corn were randomly assigned to a large
number of plots of land, and the yield per acre was computed for each plot, as
given in the table.
Yield per acre Xij for four treatments
| Method 1 |
Method 2 |
Method 3 |
Method 4 |
| 83 |
91 |
101 |
78 |
| 91 |
90 |
100 |
82 |
| 94 |
81 |
91 |
81 |
| 89 |
83 |
93 |
77 |
| 89 |
84 |
96 |
79 |
| 96 |
83 |
95 |
81 |
| 91 |
88 |
94 |
80 |
| 92 |
91 |
|
81 |
| 90 |
89 |
|
|
| |
84 |
|
|
|
The hypotheses may be stated as follows:
- H0:
The four methods are equivalent.
- H1:
Some methods of growing corn tend to give higher yields than others.
The observations are ranked from the smallest (77) of rank 1 to the largest
(101) of rank N=34.
Tied values are given average ranks.
The ranks of the observations, and the sums Ri are given below
Yields Xij for and assigned ranks Rij
|
Method 1
|
Ranks 1
|
Method 2
|
Ranks 2
|
Method 3
|
Ranks 3
|
Method 4
|
Ranks 4
|
|
83.0
|
11.0
|
91.0
|
23.0
|
101.0
|
34.0
|
78.0
|
2.0
|
|
91.0
|
23.0
|
90.0
|
19.5
|
100.0
|
33.0
|
82.0
|
9.0
|
|
94.0
|
28.5
|
81.0
|
6.5
|
91.0
|
23.0
|
81.0
|
6.5
|
|
89.0
|
17.0
|
83.0
|
11.0
|
93.0
|
27.0
|
77.0
|
1.0
|
|
89.0
|
17.0
|
84.0
|
13.5
|
96.0
|
31.5
|
79.0
|
3.0
|
|
96.0
|
31.5
|
83.0
|
11.0
|
95.0
|
30.0
|
81.0
|
6.5
|
|
91.0
|
23.0
|
88.0
|
15.0
|
94.0
|
28.5
|
80.0
|
4.0
|
|
92.0
|
26.0
|
91.0
|
23.0
|
|
|
81.0
|
6.5
|
|
90.0
|
19.5
|
89.0
|
17.0
|
|
|
|
|
|
|
|
84.0
|
13.5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni
|
9
|
|
10
|
|
7
|
|
8
|
|
G(Ri)2
|
38612.3
|
|
23409.0
|
|
42849
|
|
1482.3
|
|
G/ni
|
4290.3
|
|
2340.9
|
|
6121.3
|
|
185.3
|
|
H=12/34(35)*12937.7 - 3(35) = 21.7
making use of the fact that the test is P2
distributed with df=number of samples-1 when there are more than 5 items per
sample the critical value is 7.815
we accept H1
For two samples, the Kruskal-Wallis test is equivalent to the Mann-Whitney
test.
data table and top of second table from: http://www.stams.strath.ac.uk/~bob/classes/323/notes/whole/node91.html
INSTRUCTIONS (10 marks)
1. To be calculated manually (remember to show all work):
In 1988, Statistics Canada recognized 27 census metropolitan areas across the
nation. Among other criterion, a minimum population of 100,000 is required for
inclusion as a Canadian CMA. The following data lists the 27 CMA's in no
particular order, and provides both the population of the CMA as of June 1st,
1988, and the per capita income (PCI) of each CMA in Canadian dollars.
|
City (CMA) |
Population |
PCI in $Can. |
| |
|
Moncton |
103100 |
13700 |
|
Kitchener-Waterloo |
322400 |
16100 |
|
Calgary |
677300 |
17000 |
|
Trois Rivieres |
158600 |
12600 |
|
Sudbury |
152700 |
14500 |
|
Winnipeg |
594555 |
15700 |
|
Windsor |
259700 |
16800 |
|
Sydney |
120100 |
11100 |
|
Vancouver |
1425700 |
15400 |
|
Chicoutimi |
158600 |
12400 |
|
London |
351300 |
17000 |
|
Saskatoon |
201000 |
15200 |
|
Hamilton |
564100 |
17100 |
|
Thunder Bay |
122400 |
16900 |
|
Montreal |
2993100 |
15100 |
|
Kingston |
129200 |
16000 |
|
Edmonton |
784500 |
15200 |
|
Victoria |
262100 |
14500 |
|
St. Catharines-Niagara |
350000 |
15700 |
|
Halifax |
299000 |
16600 |
|
St. John's |
164800 |
13000 |
|
Toronto |
3536500 |
19100 |
|
Sherbrooke |
134000 |
12700 |
|
Ottawa-Hull |
843200 |
19100 |
|
Oshawa |
212700 |
17000 |
|
Saint John |
121600 |
13000 |
|
Regina |
186900 |
16000 |
1. Organize the 27 CMA's into three distinctive groups, based on the
following criteria:
a. CMA's with populations of between 100,000 and 249,999.
b. CMA's with populations of between 250,000 and 499,999.
c. CMA's with populations in excess of 500,000 inhabitants.
2. State the null and research hypotheses.
3. Determine the ranks of the CMA's.
4. Calculate the value of H by using the provided formula.
5. Do we accept or reject the null hypothesis? Why?
II. To be completed using SPSS for Windows: (10 marks)
1. Input the same data in SPSS for Windows and account for the differences
(if any) between the hand calculated H-value and the one provided by SPSS
for windows.
2. Based on the answer provided by SPSS for Windows, would you accept or
reject the null hypothesis at alpha = .05 ?
3. Be sure to hand in your output from SPSS for Windows write your name on
your copy.
Kolmogorov-Smirnov
One-Sample Test
Like the chi-square goodness of fit test, the Kolmogorov-Smirnov one-
sample test assesses the degree to which an observed pattern of categorical
frequencies differs from the pattern that would be expected on the null
hypothesis. The test statistic, here designated Dmax, is the
maximum difference between the cumulative proportions of the two patterns.
It is a more powerful alternative to chi-square
goodness-of-fit tests when its assumptions are met. Whereas the chi-square
test of goodness-of-fit tests whether in general the observed distribution is
not significantly different from the hypothesized one, the K-S test tests
whether this is so even for the most deviant values of the criterion variable.
Thus it is a more stringent test.
There is some disagreement among
statisticians whether the K-S one sample test applies only to continuous
distributions, not discrete ones such as Poisson. Most sources I consulted say a
comparison with Poisson is allowed.
The assumptions of the K-S test are as follows:
- Randomness - sample members must be randomly drawn from the population.
- Independence - Sample scores must be independent of each other.
- Measurement Scale - the categories must be ordinal or higher.
Using K-S to compare to a poisson distribution
Example
H0: the observed distribution is poisson distributed
H1: the observed distribution in not poisson distributed
Number of collisions between passenger trains on British rail, 1970 to 1983
|
year |
accidents |
|
accident class |
observed frequency |
p(x) |
|
1970 |
3 |
0 |
0 |
.017 |
|
1971 |
6 |
1 |
2 |
.070 |
|
1972 |
4 |
2 |
2 |
.141 |
|
1973 |
7 |
3 |
2 |
.192 |
|
1974 |
6 |
4 |
2 |
.195 |
|
1975 |
2 |
5 |
1 |
.160 |
|
1976 |
2 |
6 |
3 |
.110 |
|
1977 |
4 |
7 |
2 |
.063 |
|
1978 |
1 |
8+ |
0 |
.052 |
|
1979 |
7 |
sum |
14 |
1.00 |
|
1980 |
3 |
x=4.07/yr |
|
1981 |
5 |
|
1982 |
6 |
|
1983 |
1 |
| sum |
57 |
| expected |
obs cumulative prob |
exp cumulative prob |
d |
| .238 |
0 |
.017 |
-.017 |
| .098 |
.143 |
.087 |
.056 |
| 1.974 |
.286 |
.228 |
.058 |
| 2.688 |
.429 |
.420 |
.009 |
| 2.73 |
.571 |
.615 |
-.044 |
| 2.24 |
.643 |
.775 |
-.132 |
| 1.54 |
.857 |
.885 |
-.028 |
| .882 |
1.00 |
.948 |
.052 |
| .728 |
1.00 |
1.00 |
0 |
| |
|
|
dmax=.132 |
| d critical for n=14 is .349 so we accept H0 |
| |
| data from:
Chatfield, C., 1988, Problem solving: a statistician's guide, London,
Chapman and Hall, Table A.1.86. |
Problem (20 marks)
1. To be calculated manually (remember to show all work):
You may wish to use your calculations from lab 5 for the poisson
probabilities.
Lightening strikes per day were recorded in Alberta for 6
summers (July and August).
|
Strikes per day
|
Total days
|
|
0 |
209 |
|
1 |
115 |
|
2 |
32 |
|
3 |
8 |
|
4 |
1 |
Calculate using a weighted mean
|
Formula: |
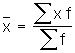
|
where
xi = observations (strikes per day)
f = weighting factor (days) |
|
For this sample, the mean is 0.567 strikes/day. |
Calculate the probability P(X) for the number of strikes per day using the
Poisson formula:
|
Strikes per day |
P(X) |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Total |
1.000 |
Now determine if the pattern of lightning strikes is consistent with a
Poisson distribution.
Introduction: Kolmogorov-Smirnov Two-Sample Test
When can you use this test?
1) With a 2-group qualitative variable (between-groups)
2) Whenever Mann-Whitney U, or the Kruskal-Wallis test could
be used.
3) Especially useful when the data contains many ties.
Its different because Mann-Whitney and
Kruskal-Wallis use ranks, Kolmogorov-Smirnov-type tests are based on .
Example
In the table below we have the average air temperatures in F
at Nottingham Castle for 1920 and 1921
H0: there is no difference in mean monthly
temperature between 1920 and 1921
H1: there is a difference in mean month temperature
between 1920 and 1921
| Month |
1920 |
cumulative prob |
1921 |
cumulative probability |
d |
| 1 |
40.6 |
.069 |
44.2 |
.073 |
-.04 |
| 2 |
40.8 |
.139 |
39.8 |
.138 |
.001 |
| 3 |
44.4 |
.215 |
45.1 |
.212 |
.003 |
| 4 |
46.7 |
.295 |
47.0 |
.289 |
.006 |
| 5 |
54.1 |
.387 |
54.1 |
.378 |
.009 |
| 6 |
58.5 |
.487 |
58.7 |
.474 |
.013 dmax |
| 7 |
57.7 |
.585 |
66.3 |
.583 |
.002 |
| 8 |
56.4 |
.681 |
59.9 |
.681 |
0.0 |
| 9 |
54.3 |
.774 |
57.0 |
.775 |
-.001 |
| 10 |
50.5 |
.860 |
54.2 |
.864 |
-.004 |
| 11 |
42.9 |
.933 |
39.7 |
.929 |
.004 |
| 12 |
39.8 |
1.00 |
42.8 |
1.00 |
0 |
| Anderson, O.D. 1976, Time Series
Analysis and Forecasting: The Box-Jenkins Approach, Butterworths, London,
pg 166. |
we accept H0
Problem (20 marks)
Below is a comparison of murder rates for 10 cities in the US for 1960 and
1970
|
1960 |
1970 |
|
10.1 |
20.4 |
|
10.6 |
22.1 |
|
8.2 |
10.2 |
|
4.9 |
9.8 |
|
11.5 |
13.7 |
| 17.3 |
24.7 |
| 12.4 |
15.4 |
| 11.1 |
12.7 |
| 8.6 |
13.3 |
| 10.0 |
18.4 |
|
From: Mendenhall, W. ,W. Ott and R.F. Larson, 1974,
Statistics: a tool for the social sciences, Boston, Duxbury Press . |
Determine if there is any difference between 1960 and 1970.
Step 1: Ho: There is no difference in the mean murder rate for
1960 and 1970.
H1: There is a difference in the mean murder rate for 1960 and
1970.
Now complete the test.
Problem: (20 marks)
Collect some data of interest and perform one of the test covered in this
exercise.