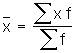
Lab Three: Measures of Central Tendency, Dispersion, Skewness and Kurtosis

INTRODUCTION

This lab presents three of the most commonly used methods available to the researcher when attempting to describe a given distribution of observations:

1) measures of central tendency (mean, mode and median) which reveal what observation(s) is (are) most representative of the entire distribution,

2) measures of dispersion (range, mean deviation, variance and standard deviation) which provide information concerning how the observations are spread out in the distribution and,

3) techniques that enable the researcher to describe the overall shape of the distribution (skewness and kurtosis measures).

An understanding of these descriptive statistics is not only directly useful but, as well, yields subsequent utility when performing parametric or non-parametric tests.

Mode: the most frequently occurring observation in a data set.

Median (Md): the middle observation of a ranked set of data.

Mean: x = Ex / n

Mean of frequencies:

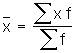
Range: the highest observation minus the lowest observation

Standard Deviation = square root of the variance

(In all cases: 'x' is an individual observation, 'E' is the summation of every individual observation 1 through I, and 'n' is the total number of observations.)

For your purposes s is the same thing as F.

skewness=

kurtosis=

Instructions:

All calibrations for the questions in Part A are to be performed using the 'life expectancy' data set and must be calculated by hand. Questions for Part B refer to the 'frost-flee days' listing and can be computed either manually or with the use of SPSS for Windows. Note: when calculating the variance, standard deviation, skewness and kurtosis values it is recommended that you construct a table similar to the example illustrated in Earickson, pg. 95.

PART A: (35 marks)

l) Calculate the mode, median and mean for the 40 countries sampled. The mean (or average) is the most commonly used measure of central tendency but what can be gained by evaluating a distribution's median or mode? Which measure of central tendency is most appropriate when nominal level data is used?

2) Calculate the range, mean deviation, variance and standard deviation. In general terms, what are each of these dispersion statistics measuring?

3) On graph paper, draw a histogram (6 classes would be most appropriate). Label on the histogram where the mean, first standard deviate (plus and minus the mean), and second standard deviate (plus and minus the mean) are located. How many of the 40 observations are within 1 standard deviation of the mean? How many observations are beyond 2 standard deviations?

4) Interpret the results attained from questions 1 through 3. (ie. What can be said about the distribution's central tendency and dispersion characteristics?)

5) What does skewness and kurtosis measure and why is it important to know the values? Calculate the skewness and kurtosis for this data set and interpret the results.

PART B:  (35 marks)

Questions:

1) What are the mean, median and mode values for the 'number of frost-free days' for the 34 stations listed above?

2) What values are calculated for: the range, mean deviation, variance, standard deviation, skewness and kurtosis?

3) To graphically show the distribution, draw a 6 class histogram.

4) With respect to the results attained in both parts A and B, which of the two data sets would be most appropriate for parametric testing? In answering this question make reference to: the derived skewness and kurtosis values and the general shape of your two histograms. (Note: one of the assumptions of parametric tests is that the underlying data set be normally distributed .)

PART C: (10 marks)

Make a list of ten numbers whose:

(List 1) mean is 75.
(List 2) mean is the same as the mean for List 1, but whose range is bigger than the range of the numbers in List 1.
(List 3) whose median is 6 and whose range is 9.
(List 4) whose mean is bigger than the median.

PART D: (20 marks)