|
  
inferential statistics
2 ways to state a statistical hypothesis
first is the null hypothesis H0, this is the
chance hypothesis
says there is no significant relationship

although the null states the difference should be zero, this
shouldn't be taken too literally, a certain amount of fluctuation is expected
question is, how big can the difference be and not be
considered significant?
to do this we use standard error

however pop std usually unknown so we use the std of the
sample

second method of stating a hypothesis is called the alternate
H1
says there is a significant difference
there are 6 steps in hypothesis testing
1) formulae the hypothesis, H0 or H1
2) specify the appropriate sample statistic and its sampling
distribution
3) select a level of significance ( ")
4) construct a decision rule
5) compute the value of the test statistic
6) make the decision
specifying the sample statistic
test statistics divided into 2 groups: parametric and
nonparametric
parametric tests are based on hypothesis concerning
population parameters
1) assumed samples are drawn form normally distributed
population
2) assumes homogeneity of variance, that is variances within
the subsamples are assumed to homogeneous from subsample to subsample, if this
is violated test is seriously compromised
3) assumed data is measured on continuous metric scale
computing test statistics
test statistics = computed statistic - hypothesized
parameter
standard error of the computed statistic
the key is the selection of the test distribution
significance of the difference between 0
and : when F
is known
use the z test

where 0
is calculated from the sample
: is the hypothesized parameter
F 0
is the standard error or the standard deviation of the sampling distributions of
the means which is computed by F/n1/2
confidence limits
how far from the population mean would the sample mean have
to deviate to cause one not to accept H0

when the random sample size is large X can be assumed to be
normally distributed
confidence limits for :
when F is
known
question might arise, how far from the population mean would
sample mean have to be to cause one not to accept H0
from knowledge of the normal distribution, regardless of
where 0 is located
relative to :,
approximately 95% of the possible values of 0
that make up the distribution are within 2 std devs of the mean
the lower and upper limits for 0
are : -1.960
and : +1.960
this is the confidence interval for :
given the sample mean 0
and Z value, the lower and upper confidence limits may be computed by

where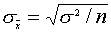
you can't be sure that population mean falls with the limits but you can 95%
confident that it does
   |